Was ist Pi eigentlich un woführ braucht man Pi?
Was ist jezt eigrntlich Pi? dafür habe ich ein kleines Experiment vorbereitet, das jeder nachmachen kann.
Dazu braucht man: 3 gleichgroße Gläser, 1 Faden, 1 Schere
Durchführung:
Nimm den Faden, wickle ihn um das Glas und schneide ihn so ab, dass er die Länge des Umfangs des Glas hat jezt stelle die gläser in einer Reie hin. Nun nehme den Faden und schaue wie viele Gläser er lkang ist
Ja gichtig ungefähr 3
Pi ist also das värhältniss zwichen Umfang und Durchmesser
U/d=π
U = Umfang
d = Durchmesser
hier auch noch ein gif was das experiment erklärt
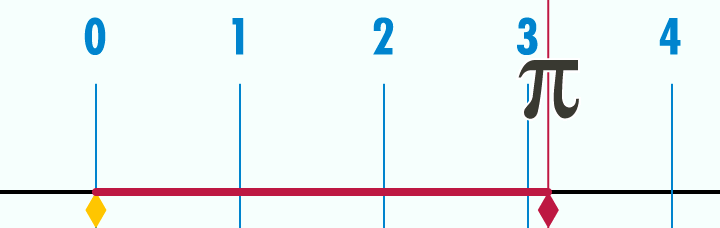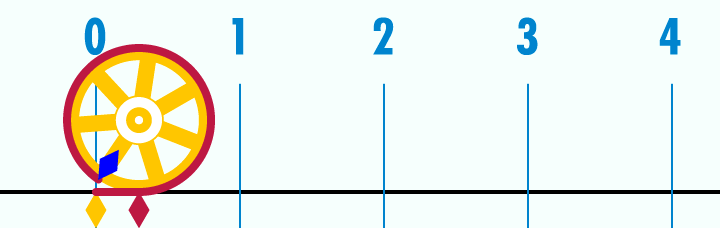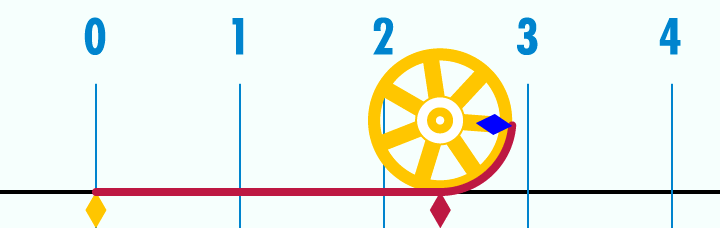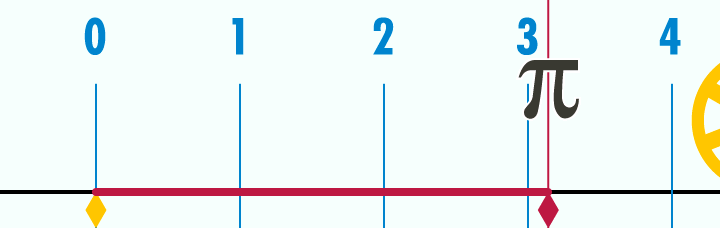
Geschichte von Pi
Laut Wikepedia:
Die Notwendigkeit, den Umfang eines Kreises aus seinem Durchmesser zu ermitteln oder umgekehrt, stellt sich im ganz praktischen Alltag – man braucht solche Berechnungen zum Beschlagen eines Rades, zum Einzäunen runder Gehege, zum Berechnen der Fläche eines runden Feldes oder des Rauminhalts eines zylindrischen Getreidespeichers. Daher suchten Menschen schon früh nach der exakten Kreiszahl und stellten immer genauere Schätzungen auf. Schließlich gelang es dem griechischen Mathematiker Archimedes um 250 v. Chr., die Zahl mathematisch einzugrenzen. In der weiteren Geschichte wurden die Versuche zur größtmöglichen Annäherung an pi phasenweise zu einer regelrechten Rekordjagd, die zuweilen skurrile und auch aufopfernde Züge annahm.Archimedes hat mit dreiecken gearbeitet
probiere es selber aus (eine kleine Spielerei)Aber wsa genau hat er gemacht?
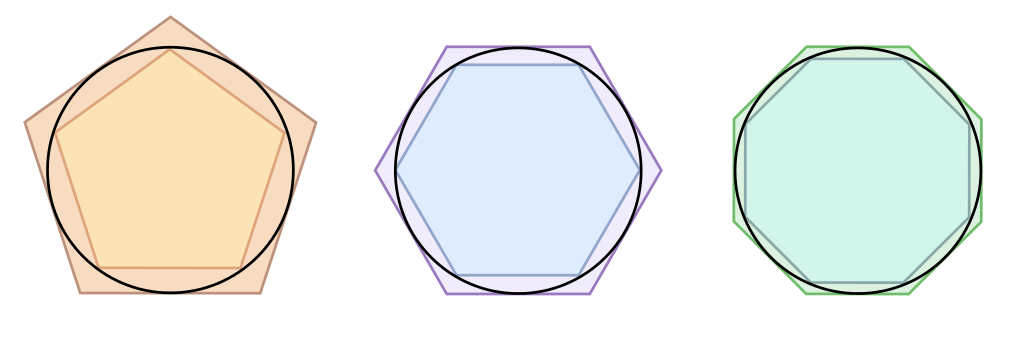
er hat ein Dreieck in und um einen Kreis Gezeichnet
in die Lücken wiederum ein 3 Eck es entstand:
6
12
mehr weniger
ect. bis 96
Da man von einem 3/6 ect. Eck den umfang messen kan doch von einem Kreis nicht. Archimedes wollte eine annäherung an Pi berechnen. Als es den Umfan des inneren und äuseren 96 Eck gemessen hatte zog er den inneren Umfang vom äuseren Umfang ab. Das ergebnidd teilte er durch 2 und addierte es zum inneren Umfang.
Rechnen mit Pi
Umfang berechnen:
U = 2π ⋅r
oder
U = π ⋅d
U = Umfang
π = 3.14159265358979323...
d = Durchmesser oder d = 2r
r = Radius
dazu eine kleine Aufgabe:
berechne den Umfang eines kreis mit dem Radius 2cm ich habe mit Pi = 3.141592653589793 gerechnet. Nimm dazu einen Tschenrechner im Kopf ist das etews achwierig
Hast du ein anderes Ergebniss? Dan drücke
hier wenigerre
um Hilfe zu erhalten